原文链接:go leetcode,php 代码个人原创
x 的平方根(Qqrtx)
题干:
实现 int sqrt (int x) 函数。 计算并返回 x 的平方根,其中 x 是非负整数。 由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。 示例 1: 输入: 4 输出: 2 示例 2: 输入: 8 输出: 2 说明: 8 的平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。 来源:力扣
解题思路
一个 大于 1 的正整数,记为 x,它的平方根一定是 大于等于 1,且小于等于 x 的二分之一,区间表示为 [1, x/2],由于题目规定 只保留整数部分,所以基于上面的分析,求平方根实际变成了:在 [1, x/2] 有序序列中寻找一个正整数 number。分析到这里,是不是觉得和 让我们一起啃算法 —- 搜索插入位置 有点像。
其实对于 在一个有序序列(如果无序,可以先对序列排序)中找某一个数 的题型都可以使用 二分查找 的解题思路。
首先我们初始化 left 为 1, right 为 x / 2(取整数), mid = left + (right - left) / 2,V 为 mid * mid。
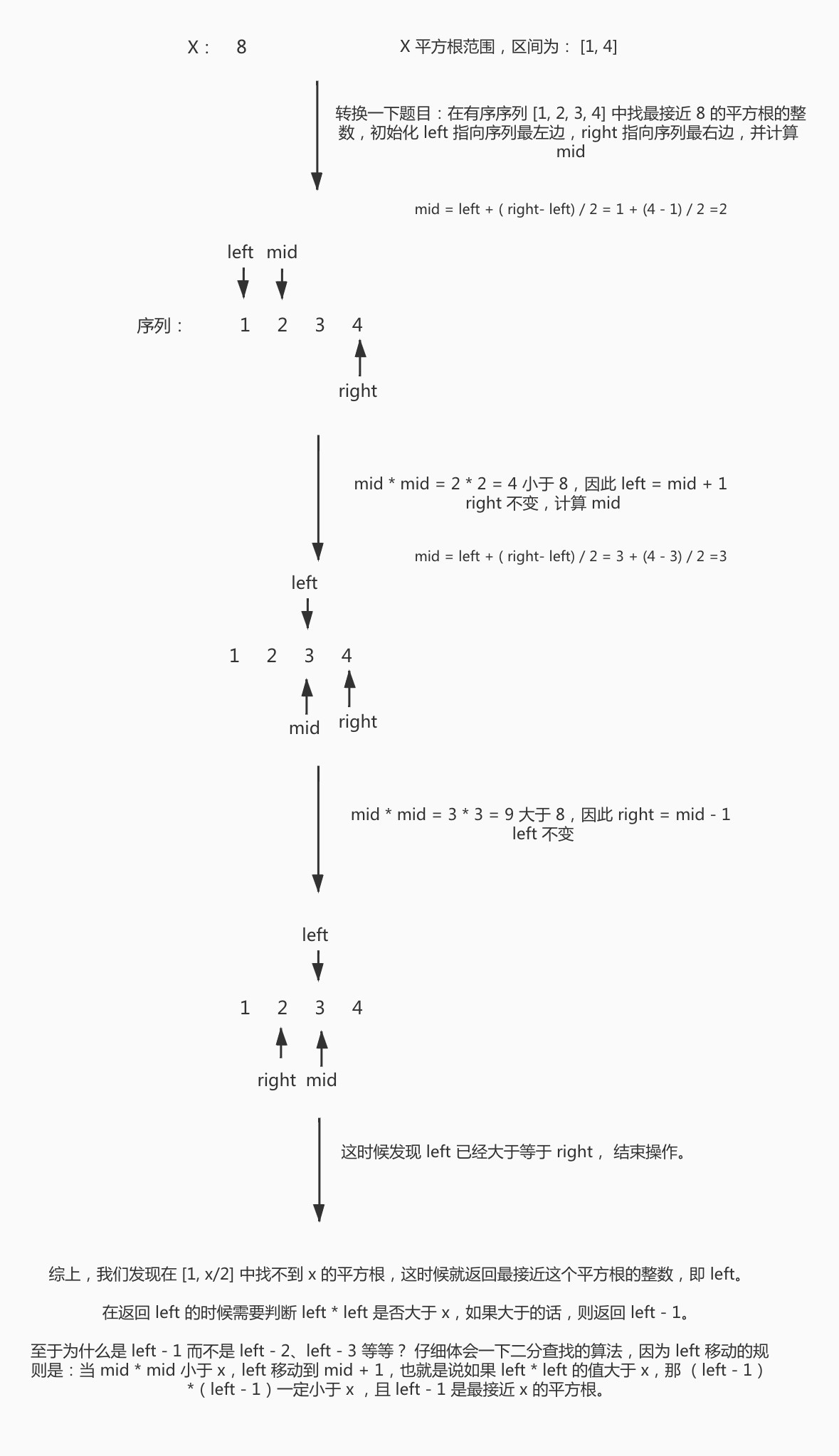
接着判断 V 与 x 的大小。如果 V 小于 x,那么将 left 设置为 mid + 1,right 不变,重新计算 mid 并重复上面的比较。如果 V 大于 x,那么将 right 设置为 mid - 1,left 不变,重新计算 mid 并重复上面的比较。如果 V 等于 x,则返回 mid。直到 left >= right,表明在 [1, x/2] 中找不到一个整数恰好等于 x 的平方根,这时候就返回最接近这个平方根的整数,即 left。
注:在返回 left 的时候需要判断 left * left 是否大于 x,如果大于的话,则返回 left - 1。
流程图如下:
Go 实现
// 二分查找 主要是操作 数组的索引。
// 本题区间 [1, x/2] 因为是连续的正整数,完全可以当作数组的索引使用,所以二分查找可以直接使用,不需要做什么转换
func mySqrt(x int) int {
left := 1
right := x / 2
for left < right {
// 中间值
mid := left + (right - left) / 2
// 如果 中间值的平方 小于x,则移动left到mid的后一位
if mid * mid < x {
left = mid + 1
} else if mid * mid > x {
// 如果 中间值的平方 大于x,则移动right到mid的前一位
right = mid - 1
} else {
// 相等的话,mid就是x的平方根
return mid
}
}
// 判断当前left的平方是否大于x
if left * left > x {
return left - 1
}
return left
}
PHP 实现
function mySqrt($x) {
if($x <= 1) {
return $x;
}
$left = 1;
$right = $x;
while($left < $right) {
$mid = $left + (int)(($right - $left) / 2) + 1;
if($mid * $mid > $x) {
$right = $mid - 1;
} else {
$left = $mid;
}
}
return $right;
}
echo mySqrt(4); // output: 2
最后恰饭 阿里云全系列产品/短信包特惠购买 中小企业上云最佳选择 阿里云内部优惠券